https://www.acmicpc.net/problem/4256
목적
이진트리의 전위 순회와 중위 순회 결과가 주어졌을 때, 후위 순회 결과를 구하자.
접근법
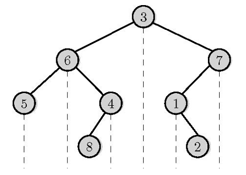
1. 다음 그림을 보자.

- 3은 루트 노드, 파란 부분과 노란 부분은 각각 루트 노드의 왼쪽과 오른쪽 노드들이다.
- 세번째 후위 순위의 그림을 보면, 나머지는 어떤 수인지 몰라도, 파란 부분의 노드들과 노란 부분의 노드들 순으로 나온뒤에, 루트 노드가 맨 마지막으로 나온다는 것을 알 수있다.
2. 두 가지의 배열(전위, 중위 순회)로 어떻게 마지막과 같은 형태로 만들 수 있을까?(아래 코드의 sol() 함수 참고...)
- 부분 트리 단위로 접근해야하며, 이를 재귀적으로 구현한다.
- 전위 순회 배열을 부분 트리로 이용할 것이며, 중위 순회 배열은 부분 트리의 경계(왼쪽,오른쪽)를 한정하는 데 사용하자.
- 부분 트리의 첫번째 인덱스는 현재의 부분 트리의 루트 노드로서, 왼쪽 부분 트리와 오른쪽 부분 트리의 처리가 끝난 뒤에 출력을 해야한다.
- 중위 순회에서 루트 노드의 인덱스 위치로 각 부분 트리의 경계를 결정하고 이를 재귀적으로 반복하자. (중위 순회 배열을 노드 번호에 따른 인덱스 위치를 알 수 있도록 바꿔 저장한다.)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<bits/stdc++.h>
#define f(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
int a[1001], b[1001];
void sol(int i, int l, int r) {
if (l > r)return;
if (l == r) {
cout << a[i] << ' ';
return;
}
int tmp = b[a[i]];
sol(i + 1, l, tmp - 1);
sol(i + tmp - l + 1, tmp + 1, r);
cout << a[i] << ' ';
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int t; cin >> t;
while (t--) {
int n; cin >> n;
f(i, 1, n)cin >> a[i];
f(i, 1, n) {
int tmp; cin >> tmp;
b[tmp] = i;
}
sol(1, 1, n);
cout << '\n';
}
return 0;
}
|

문제 설명과 코드에 대한 피드백은 언제나 환영합니다.
다양한 의견 댓글로 남겨주세요.
'Problem Solving > BOJ 백준' 카테고리의 다른 글
| [ BOJ 백준 1949번 - 우수 마을 ] 해설 및 코드 (0) | 2020.01.02 |
|---|---|
| [ BOJ 백준 1967번 - 트리의 지름 ] 해설 및 코드 (0) | 2020.01.02 |
| [ BOJ 백준 2250번 - 트리의 높이와 너비 ] 해설 및 코드 (0) | 2019.12.30 |
| [ BOJ 백준 16437번 - 양 구출 작전 ] 해설 및 코드 (0) | 2019.12.30 |
| [ BOJ 백준 4803번 - 트리 ] 해설 및 코드 (0) | 2019.12.30 |



